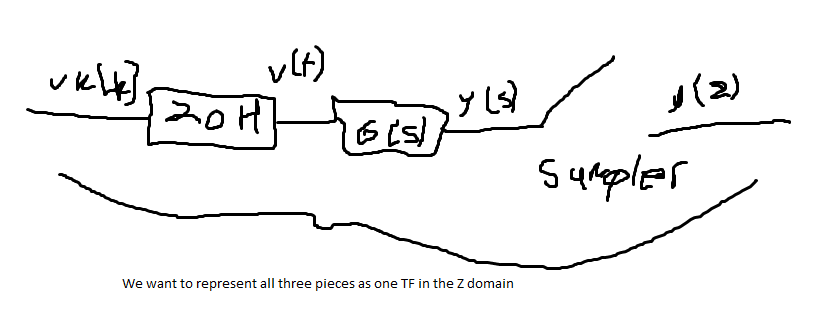
A key insight is that each hold between samples can be represented by the sum of two step functions. With this insight, our discrete signal vk[k] is turned into a continous signal by multiplying each sample by {a step function minus a step function shifted right one}, which gives a one T pulse of height zk[k]!
$$v(t) = \sum^{inf}_{k=0} v_k[k] *( U(t-kT) - U(t-(k+1)T))$$ Now, we can take the laplace transform of our signal so that it is in the same domain as G(s) (knowing that Laplace transform of a step is 1/s): $$L(s) = \sum^{inf}_{k=0}vk[k](\frac{1}{s} e^{-kT} - \frac{1}{s}e^{-(k+1)T})$$ Y(s) is just G(s)L(s): $$Y(s) = \frac{1-e^{-Ts}}{s}G(s)\sum_{k=0}^{inf}V_ke^{-kTs}$$ Using the definition of the Z-transform(look at that section for review), we can substitute the sum for the Z transform of Vk! Also, all e^-Ts are equal to z by definition: $$\frac{Y(s)}{V(z)} = \frac{z-1}{z} \frac{G(s)}{s}$$ And taking a z transform of the s-term to get it in discrete domain: $$\frac{Y(z)}{V(z)} = \frac{z-1}{z} Z(\frac{G(s)}{s})|_{t=kT}$$ As an example: let G(s) be 1/s+1. $$\frac{z}{z-1} * Z(\frac{G(s)}{s}) = \frac{1-e^{-T}}{z-e^{-T}}$$